This is a continuation of the Mechanical UT Scanner project. Out of curiousity, I wanted to see how my educated guess of using 8 gauge (0.1285” | 3.26mm ) aluminum sheet metal would hold up to the bumps and impacts of transporting the tool (these would be far greater than the forces exerted during operation).

Boundary Conditions

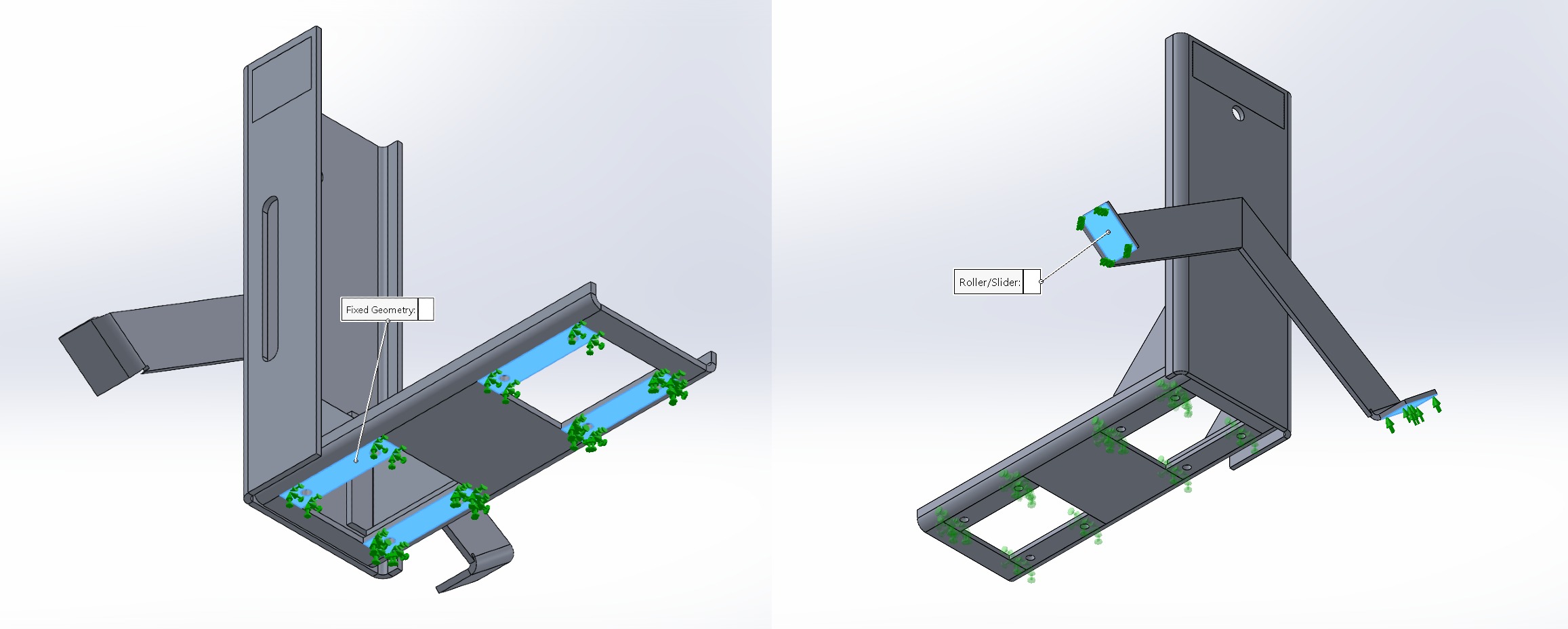
As an initial litmus test, let’s see the displacement and stresses by appling 200N / 45 lbs-force (to simulate a careless shove from a rough-and-tough technician) to the leading top edge of the frame. We’re using SolidWorks Simulation which admitedly is not the best for running Finite Element Analysis so we’ll need to hack our design a bit. We need to start of by choosing our boundary conditions and specifying our fixtures.

Even though a sideways force would realistically be mainly transferred to the side arm, as mentioned in the original post, the side arms were not part of the scope, so we set the bearing-mounts on the base fame as fixed geometry so most of the force is transferred through the frame. This would be like clamping the base down and pushing on the top frame, which could happen during assembly on site. We use roller fixtures on the sidearm to analysis any resultant stresses to confirm our assumptions of the forces going mainly through the base frame.

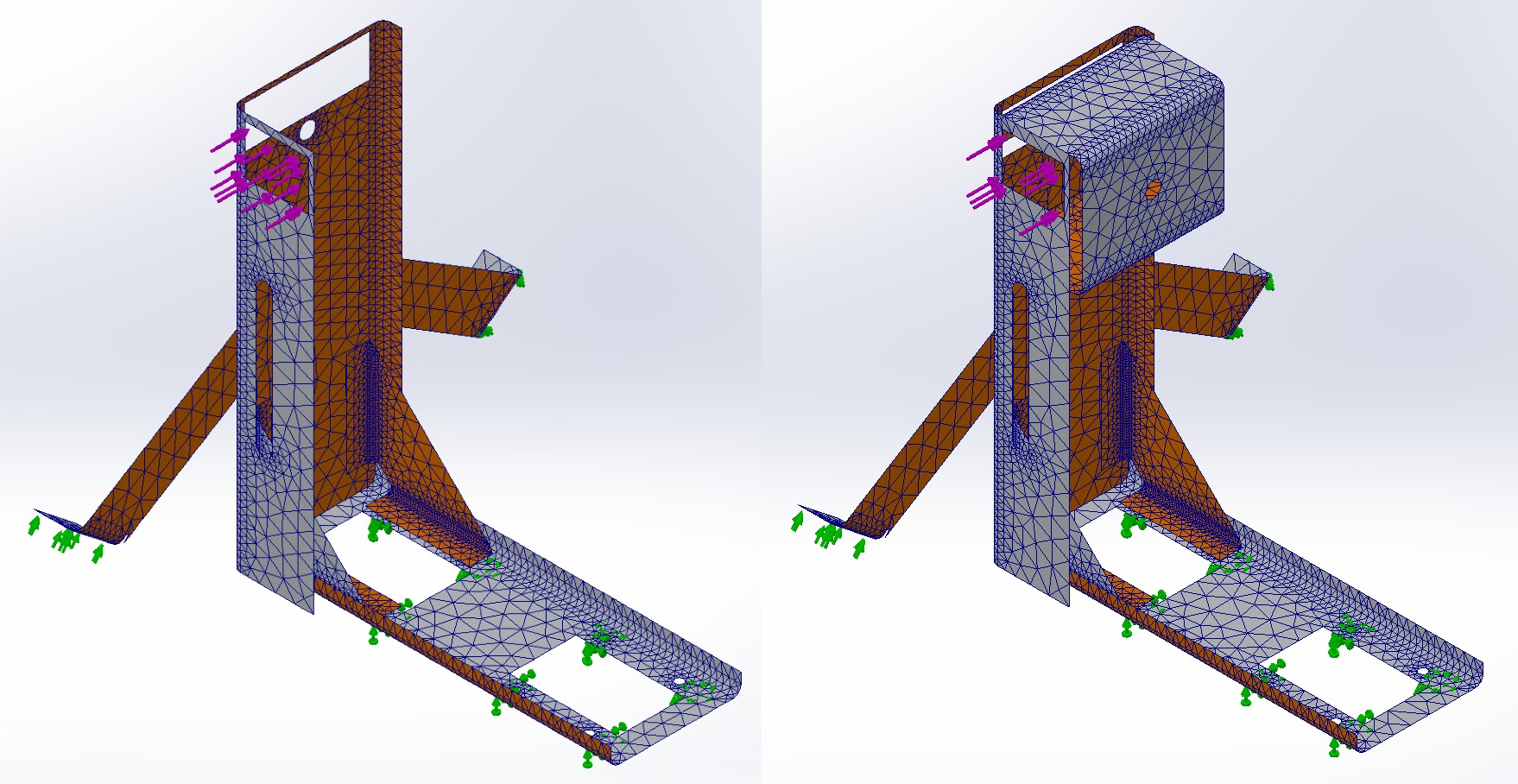
Meshes and Loads

For the mesh, because this is a quick simulation to see resultant forces, we skip things such as doing mesh-independent studies to confirm the mesh size is fine enough. We’re using a shell mesh using mid-surfaces and high quality mesh settings, this gives us a minimum element size of 0.0215” in the bends and maximum of 0.429” on the flat surfaces.

For the forces, I had to create a 0.01” extruded cut on the main frame to create a surface to apply the load to, so it won’t show in the resultant simulations but it’s there.

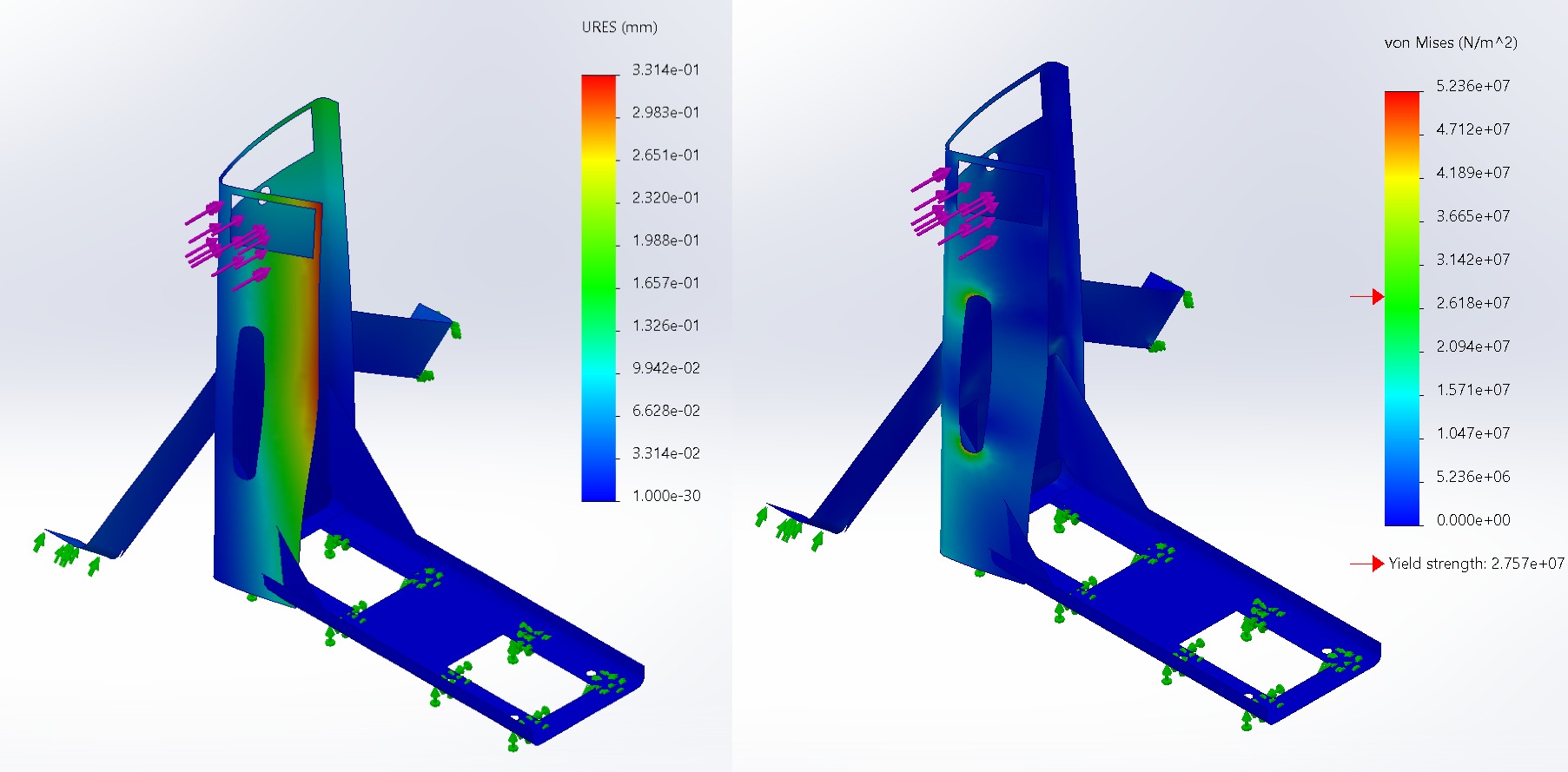
First Simulation without Gear House

After running the simulation for just the main frame, we see the left graph below shows the displacement with a maximum of 0.013” or 0.33mm. This seems like nothing but if you look at the maximum stress on the right, you’ll see it’s 52.4 MPa - Aluminum 1060 was used for this simulation and has a yield stress of about 27.6 MPa. We’ll get into this result at the end but let’s now compare these values if we add in the gear housing structure.

Second Simulation with Gear House

With the support of the gear house, the maximum displacement drops to 0.0071” or 0.18mm. And the maximum stress drops to 33.6 MPa, much closer to the yield strength of 27.6 MPa.

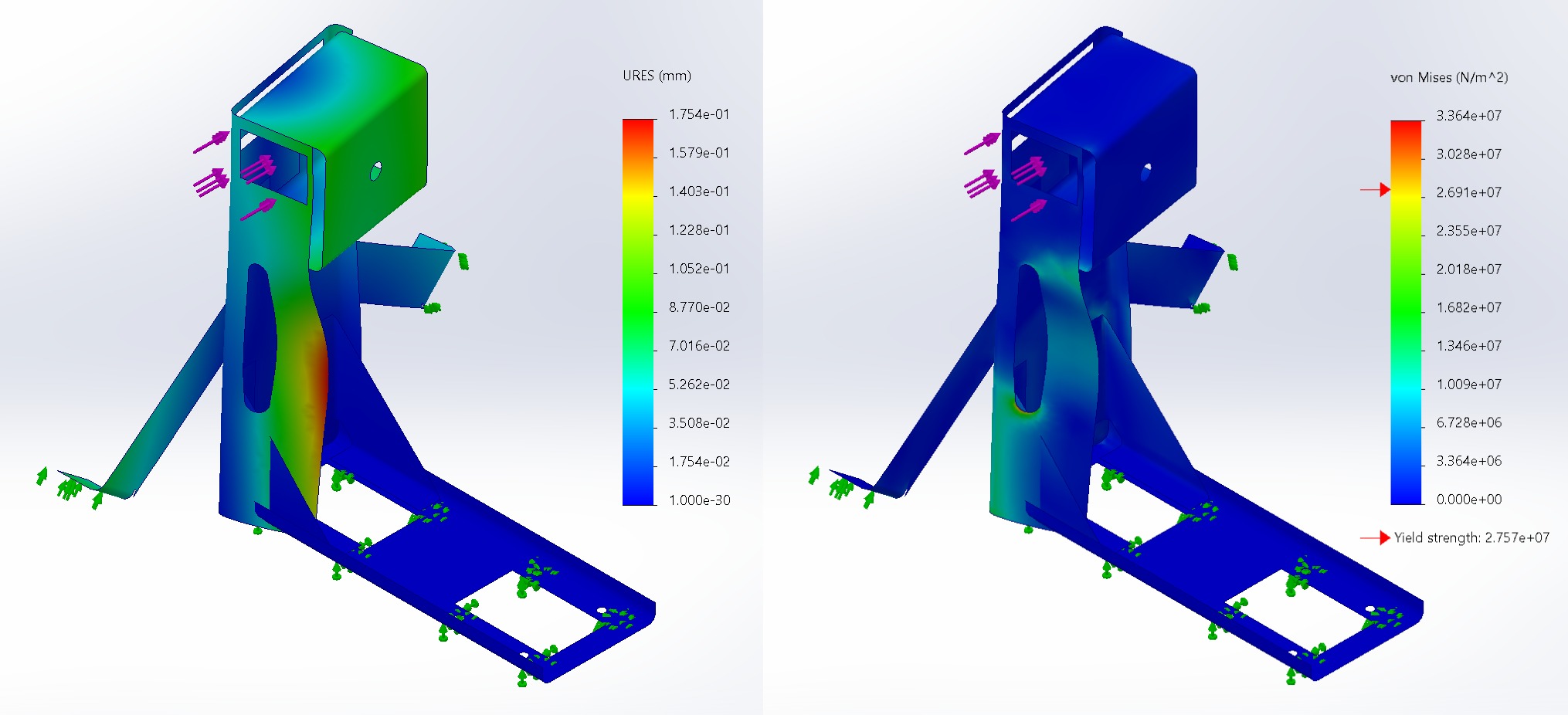
So is the current frame design not strong enough since the max stress is larger than the material’s yield stress? Not necessarily. It’s important to keep in mind that simulations work with ideal cases, so imperfections in the real world would likely lower the overall strength of the material. However, the max strain occurs in the slot used to locate the pulley below, and that is not necessarily an issue, which we can get into below.

Close Up of Stress in Slot

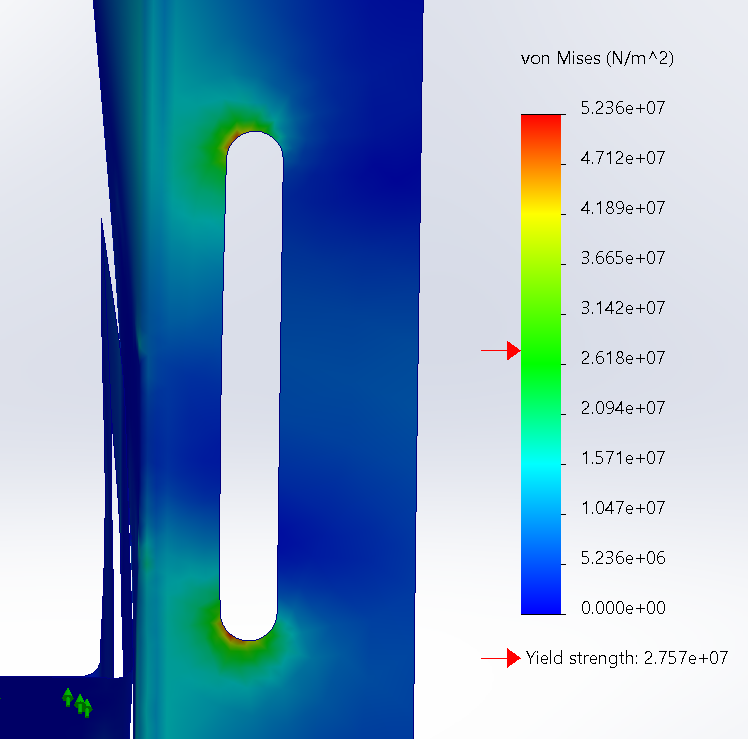
As can be seen in the above image, the ends of the slots act as stress amplifiers, causing the material to exceed it’s yield strength. Interestingly this is how fracture mechanics work and can be used to predict the fatigue life of materials based on initial crack lengths and cyclical forces. Anyways, once the material exceeds it’s yield strength, localized hardening of the material will occur known as strain or work hardening. This will cause the material to gain a new yield strength. You can see this depicted in the graph below. Basically what’s happening is a bunch of crack dislocations are forming in the material that are making it harder for more cracks to propagate. The downside is that the material loses ductility (seen by the smaller area under the graph of the strain-hardened material).

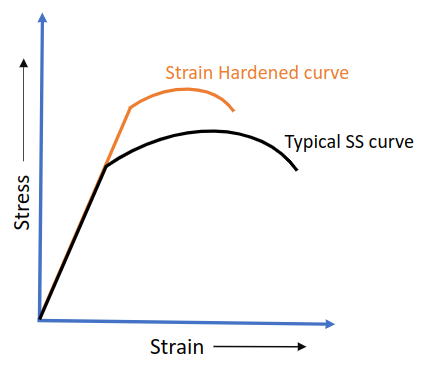
So in reality, this material and thickness should be good enough and due to the low-cost of aluminum sheet metal, it’s worth getting this made to test than spend more time on simulations. The above served as a quick sanity check however. If this part was a lot more complex, or consequences of failure were higher, then this would be different.